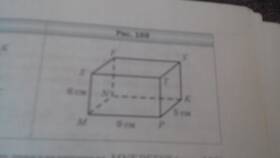
Прямоугольный параллелепипед - это объемная фигура с шестью прямоугольными гранями. Рассмотрим основные методы вычисления различных характеристик этой геометрической фигуры.
Содержание
Прямоугольный параллелепипед - это объемная фигура с шестью прямоугольными гранями. Рассмотрим основные методы вычисления различных характеристик этой геометрической фигуры.
Основные параметры прямоугольного параллелепипеда
- Длина (a)
- Ширина (b)
- Высота (c)
Формулы для вычисления
| Характеристика | Формула | Обозначения |
| Площадь поверхности | S = 2(ab + bc + ac) | a, b, c - измерения |
| Объем | V = a × b × c | a, b, c - измерения |
| Сумма длин всех ребер | L = 4(a + b + c) | a, b, c - измерения |
Пошаговый алгоритм вычисления суммы длин ребер
- Измерьте длину (a), ширину (b) и высоту (c) параллелепипеда
- Сложите все три измерения: a + b + c
- Умножьте полученную сумму на 4
- Результат будет равен сумме длин всех 12 ребер параллелепипеда
Пример расчета
| Параметр | Значение |
| Длина (a) | 5 см |
| Ширина (b) | 3 см |
| Высота (c) | 2 см |
| Расчет | 4 × (5 + 3 + 2) = 4 × 10 = 40 см |
Особые случаи
Куб как частный случай
Для куба (где a = b = c):
- Сумма длин ребер: L = 12a
- Площадь поверхности: S = 6a²
- Объем: V = a³
Вычисление диагонали
Формула пространственной диагонали:
d = √(a² + b² + c²)
Практическое применение
| Область | Применение |
| Строительство | Расчет материалов для каркаса |
| Упаковка | Определение длины скрепляющей ленты |
| Производство | Расчет металлопроката для конструкций |
Важные замечания
- Все измерения должны быть в одинаковых единицах
- Для точных расчетов используйте точные значения измерений
- При работе с реальными объектами учитывайте возможные отклонения формы
- Проверяйте правильность подстановки значений в формулы
